 /
/ 
Time Limit: 2 sec / Memory Limit: 256 MB
問題文
あなたは、N 頂点 M 辺の無向グラフを持っています。グラフは連結で、自己ループや多重辺はありません。頂点は 1 から N まで番号が振られており、辺は 1 から M まで番号が振られています。
最初、辺はすべて白です。あなたは、「白い辺をひとつ選び、オレンジに塗る」という操作を繰り返し行います。ただし、オレンジの辺のみからなる奇数長の閉路ができてしまうような操作は行えません。
あなたは、可能な操作があるかぎりは操作を行い続けます。あなたが操作を終えた後、最終的な辺の色の組合せとして考えられるものは何通りか求めてください。
入力
入力は以下の形式で標準入力から与えられる。
N M x_1 y_1 x_2 y_2 : x_M y_M
- 1 行目には、グラフの頂点数 N (2≦N≦16) と辺数 M (N-1≦M≦N(N-1)/2) が空白区切りで与えられる。
- 2 行目からの M 行には、辺の情報が与えられる。このうち i 行目には、i 番目の辺の端点 x_i と y_i (1≦x_i<y_i≦N) が空白区切りで与えられる。
- i≠j ならば、x_i≠x_j または y_i≠y_j である。
- グラフは連結である。
出力
あなたが操作を終えた後、最終的な辺の色の組合せとして考えられるものは何通りか出力せよ。出力の末尾には改行を入れること。
入力例1
3 3 1 2 1 3 2 3
出力例1
3
図の 3 通りです。
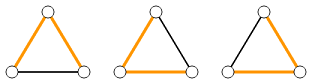
入力例2
4 5 1 2 1 3 1 4 2 4 3 4
出力例2
5
図の 5 通りです。

入力例3
5 4 1 2 2 3 3 4 4 5
出力例3
1
図の 1 通りです。

Problem
You are given an undirected graph with N vertices and M edges. It is connected and has no self-loops nor parallel edges. The vertices are numbered from 1 to N, and the edges are numbered from 1 to M.
Initially, all the edges are white. You repeat the following operation: Choose a white edge and paint it in orange. However, you are not allowed to apply an operation that yields an odd-length cycle that consists only of orange edges.
You repeat the procedure until there is no valid operation. Your task is, given the initial graph, to compute the number of possible outcomes (i.e., the colors of the edges).
Input
The input is given from the standard input in the following format.
N M x_1 y_1 x_2 y_2 : x_M y_M
- In the first line, integers N (2≦N≦16) and M (N-1≦M≦N(N-1)/2) are written, separated by a space. N and M describe the numbers of vertices and edges, respectively.
- The subsequent M lines describe the edges. The i-th line among them contains two integers x_i and y_i (1≦x_i<y_i≦N), separated by a space, which indicates the endpoints of edge i.
- If i≠j, then x_i≠x_j or y_i≠y_j.
- The graph is connected.
Output
Output the number of possible outcomes, i.e., the number of the possible sets of orange edges. Put the newline at the end of the output.
Input Example 1
3 3 1 2 1 3 2 3
Output Example 1
3
There are three possible outcomes as illustrated in the figure below.

Input Example 2
4 5 1 2 1 3 1 4 2 4 3 4
Output Example 2
5
There are five possible outcomes as illustrated in the figure below.

Input Example 3
5 4 1 2 2 3 3 4 4 5
Output Example 3
1
There is one possible outcome as illustrated in the figure below.
